Surface area of prisms and cylinders maze answer key – Embark on an intriguing exploration of the surface area of prisms and cylinders through a captivating maze answer key. This interactive guide seamlessly blends mathematical concepts with a touch of adventure, making the learning process both enjoyable and enlightening.
As you navigate the maze, you will encounter a series of challenges that require you to apply formulas and understand the relationship between the dimensions of prisms and cylinders and their surface areas. Each correct path leads to a deeper understanding of these geometrical shapes, while the answer key provides clear explanations and step-by-step solutions.
Surface Area of Prisms
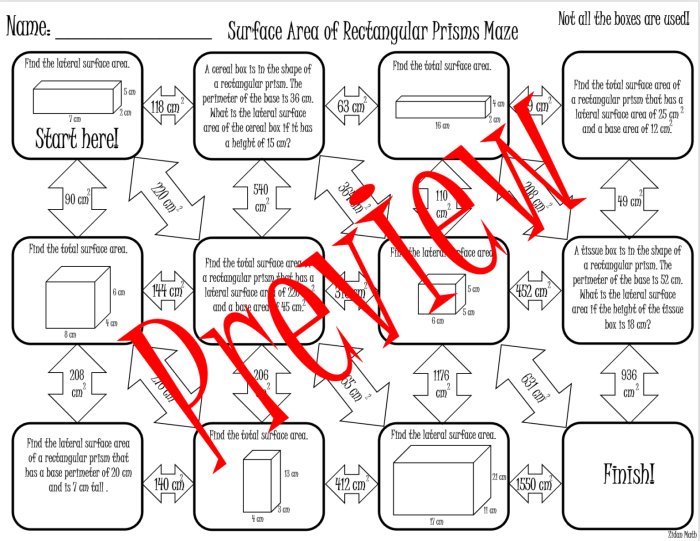
Prisms are three-dimensional shapes with two parallel faces, called bases, and rectangular faces, called lateral faces. The surface area of a prism is the sum of the areas of its bases and lateral faces.The formula for calculating the surface area of a prism is:“`Surface Area = 2B + PL“`where:* B is the area of one base
- P is the perimeter of the base
- L is the height of the prism
Types of Prisms and Their Surface Areas
There are different types of prisms, each with its own formula for calculating the surface area.*
-*Rectangular Prism
A rectangular prism has six rectangular faces. The formula for calculating its surface area is:“`Surface Area = 2(lw + lh + wh)“`where:* l is the length of the prism
- w is the width of the prism
- h is the height of the prism
*
-*Triangular Prism
A triangular prism has two triangular bases and three rectangular faces. The formula for calculating its surface area is:“`Surface Area = 2(1/2bh + bl + lh)“`where:* b is the base of the triangular prism
- h is the height of the triangular prism
- l is the length of the rectangular faces
- w is the width of the rectangular faces
*
-*Circular Prism
A circular prism has two circular bases and rectangular faces. The formula for calculating its surface area is:“`Surface Area = 2πr² + 2πrh“`where:* r is the radius of the circular bases
h is the height of the prism
Table of Surface Area Formulas for Different Types of Prisms, Surface area of prisms and cylinders maze answer key
| Type of Prism | Formula ||—|—|| Rectangular Prism | 2(lw + lh + wh) || Triangular Prism | 2(1/2bh + bl + lh) || Circular Prism | 2πr² + 2πrh |
Surface Area of Cylinders: Surface Area Of Prisms And Cylinders Maze Answer Key
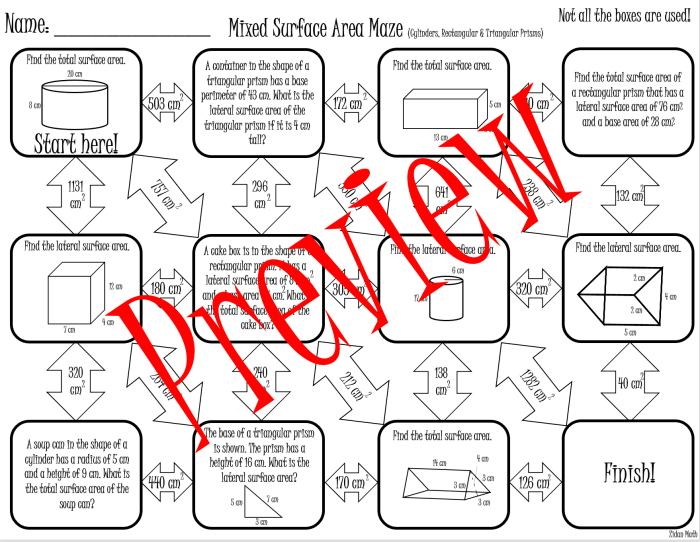
A cylinder is a three-dimensional shape with two parallel circular faces, called bases, and a curved surface. The surface area of a cylinder is the sum of the areas of its bases and curved surface.The formula for calculating the surface area of a cylinder is:“`Surface Area = 2πr² + 2πrh“`where:* r is the radius of the circular bases
h is the height of the cylinder
Relationship between Radius, Height, and Surface Area of a Cylinder
The radius and height of a cylinder have a direct relationship with its surface area. As the radius increases, the surface area also increases. Similarly, as the height increases, the surface area also increases.
Illustration of a Cylinder with Surface Area Labeled
[Image of a cylinder with its surface area labeled]
Frequently Asked Questions
What is the formula for calculating the surface area of a prism?
The surface area of a prism is calculated by adding the areas of all its faces. For a rectangular prism, the formula is: SA = 2(lw + lh + wh), where l is the length, w is the width, and h is the height.
How is the surface area of a cylinder related to its radius and height?
The surface area of a cylinder is calculated using the formula: SA = 2πr(r + h), where r is the radius and h is the height. The surface area increases as either the radius or height increases.